In the vast world of linear algebra, linear transformations form a cornerstone concept that bridges the gap between abstract mathematics and real-world application. Whether you’re designing mechanical systems, visualizing rotations in 3D space, or simplifying multidimensional data, understanding linear transformations is essential. This article delves deeply into what a linear transformation is, how it works, how to compute its kernel, and how it’s taught in a Linear Algebra Bachelor of Engineering Book.
📘 What Is a Linear Transformation?
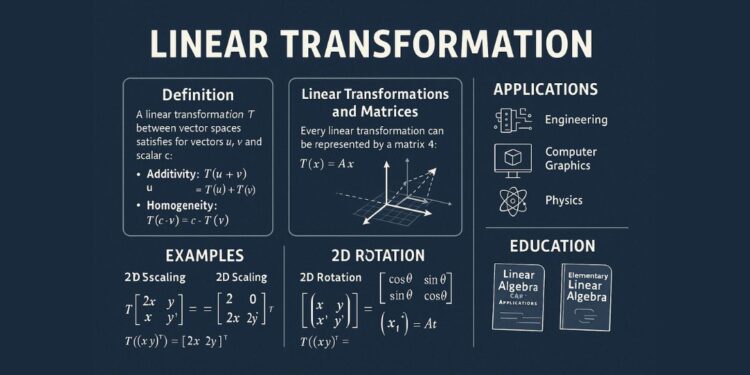
Let’s begin with a formal definition.
A linear transformation is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. Suppose T : V → W is a function where V and W are vector spaces. Then T is a linear transformation if for any vectors u, v ∈ V and scalar c ∈ ℝ, the following hold:
- Additivity: T(u + v) = T(u) + T(v)
- Homogeneity: T(c · v) = c · T(v)
In essence, linear transformations maintain the “shape” and structure of mathematical operations between spaces.
🧠 Linear Transformations and Matrices
Every linear transformation in finite-dimensional vector spaces can be represented by a matrix. Given a matrix A and a vector x, the transformation can be written as:
T(x) = A · x
This representation allows transformations like:
- Rotations
- Reflections
- Scaling
- Projections
to be expressed algebraically and visualized geometrically. Matrix multiplication becomes the tool to apply these transformations.
📐 Examples of Linear Transformations
Let’s look at a few common examples:
✅ Example 1: 2D Scaling
T([x y]ᵗ) = [2 0] [x] = [2x]
[0 2] [y] [2y]
This transformation scales every vector by a factor of 2.
✅ Example 2: 2D Rotation
T([x y]ᵗ) = [cos(θ) -sin(θ)] [x]
[sin(θ) cos(θ)] [y]
This rotates a vector by angle θ about the origin.
📖 Linear Transformations in Engineering Education
In a Linear Algebra Bachelor of Engineering Book, linear transformations are introduced early due to their wide applications in engineering disciplines:
- Electrical Engineering: State-space analysis and control systems
- Mechanical Engineering: Stress-strain transformations
- Computer Engineering: 3D graphics and simulations
- Civil Engineering: Load analysis in structures
Popular engineering-focused textbooks include:
- Linear Algebra and Its Applications by David C. Lay
- Elementary Linear Algebra by Howard Anton
- Introduction to Linear Algebra by Gilbert Strang
These books offer real-world applications of linear transformations, reinforced with matrix examples, code implementations, and mechanical simulations.
🔍 How to Find the Kernel of a Linear Transformation
The kernel (or null space) of a linear transformation T : V → W is the set of all vectors in V that map to the zero vector in W. Formally:
Ker(T) = { v ∈ V | T(v) = 0 }
✏️ Why It Matters:
- The kernel indicates the loss of dimension or collapse in transformation.
- If the kernel is only the zero vector, the transformation is injective (one-to-one).
🧮 Steps to Find the Kernel
Let’s break down the process with an example:
Example:
Let A =
[1 2] [3 6]
We want to find all vectors x such that:
A · x = 0 ⇒ [1 2] [x₁] = [0]
[3 6] [x₂] [0]
This yields:
- x₁ + 2x₂ = 0
- 3x₁ + 6x₂ = 0
Second equation is redundant. Solving the first:
x₁ = −2x₂
So the kernel is:
Ker(T) = span { [-2]
[ 1] }
This subspace includes all vectors that vanish under the transformation T.
🔗 Applications of Linear Transformations
📊 1. Data Science
- Principal Component Analysis (PCA) uses linear transformations to reduce dimensionality while preserving variance.
🎮 2. Computer Graphics
- All 3D object movements—rotations, translations, scaling—are performed via transformation matrices.
🧲 3. Physics & Quantum Mechanics
- Operators in quantum mechanics (like position and momentum) are linear transformations.
🧱 4. Civil & Mechanical Engineering
- Finite Element Analysis (FEA) uses matrices and transformations to analyze structures.
🛠️ Key Properties of Linear Transformations
| Property | Description |
|---|---|
| Additivity | T(u + v) = T(u) + T(v) |
| Homogeneity | T(c ⋅ v) = c ⋅ T(v) |
| Matrix Representation | T(x) = Ax |
| Kernel | Set of vectors mapped to zero |
| Image | Set of vectors reachable by the transformation |
📝 Quick Checklist for Understanding Linear Transformations
✅ Can you identify whether a function is linear (does it preserve addition and scalar multiplication)?
✅ Can you write the matrix that represents a transformation?
✅ Can you compute the kernel and determine its dimension (nullity)?
✅ Do you understand what transformations look like geometrically (e.g., scaling, rotation, projection)?
📚 Additional Learning Resources
- Khan Academy: Free video lectures on linear transformations
- 3Blue1Brown (YouTube): Intuitive animated visualizations of linear algebra
- WolframAlpha: Symbolic calculator for transformations and kernels
📓 Summary
Linear transformations provide a consistent, powerful framework for analyzing how systems, vectors, and dimensions interact and change. Whether you’re compressing datasets, rotating 3D models, or solving systems of equations in physics, this concept is invaluable.
For more in-depth guides, examples, and linear algebra study materials, visit Pure Acad, your learning partner for mastering foundational mathematical concepts.