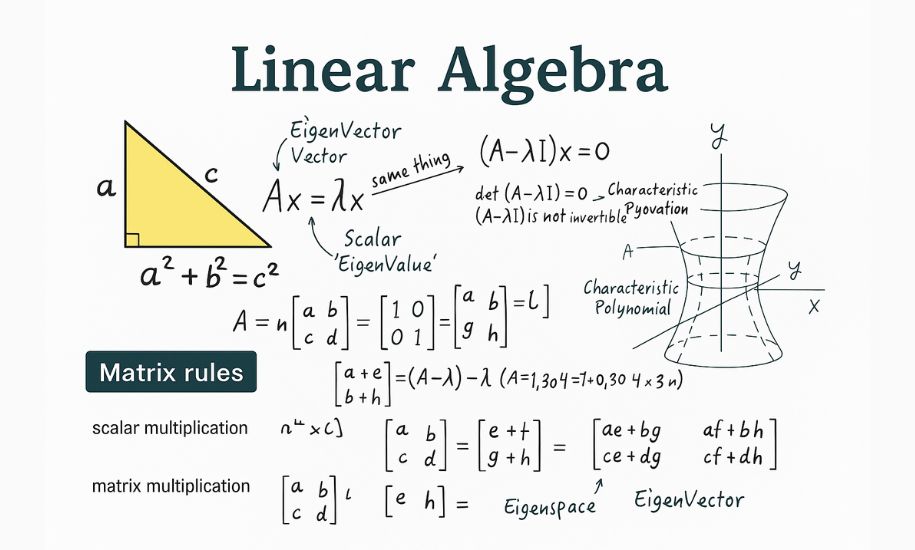
Linear Algebra is one of the most powerful and essential branches of mathematics, forming the foundation of countless modern applications in science, technology, engineering, and beyond. This article explores “What is Linear Algebra?”, its core concepts, popular textbooks, practical examples, problem solutions, and real-world applications.
🔍 What is Linear Algebra?
Linear Algebra is a branch of mathematics that focuses on vector spaces and linear mappings between such spaces. It involves studying lines, planes, and subspaces, but extends far beyond geometry to systems of equations, transformations, and data structures.
At its core, linear algebra deals with:
- Vectors (quantities with magnitude and direction)
- Matrices (arrays of numbers representing linear transformations)
- Systems of Linear Equations (multiple linear equations that relate variables)
- Vector Spaces and Subspaces
- Eigenvalues and Eigenvectors
These components enable mathematicians, scientists, and engineers to solve problems in fields ranging from machine learning to physics and economics.
🧠 Core Concepts in Linear Algebra
1. Vectors and Vector Spaces
Vectors represent quantities and can be visualized in one or multiple dimensions. A vector space is a set of vectors closed under addition and scalar multiplication, forming the foundational structure for linear algebra.
2. Matrices and Matrix Operations
Matrices are rectangular arrays of numbers used to perform linear transformations. Key operations include:
- Matrix addition and subtraction
- Matrix multiplication
- Determinants and inverses
- Transposes and identity matrices
3. Systems of Linear Equations
Solving multiple linear equations simultaneously is a major function of linear algebra. Techniques include:
- Gaussian elimination
- Matrix inversion
- Cramer’s Rule
4. Eigenvalues and Eigenvectors
Eigenvectors are special vectors that only scale (not rotate) when a linear transformation is applied. The corresponding scale factor is the eigenvalue. These concepts are essential in quantum physics, facial recognition, and more.
5. Linear Transformations
A linear transformation maps vectors from one space to another while preserving vector addition and scalar multiplication. It’s the backbone of data manipulation and transformation in computing.
📚 Best Linear Algebra Books
Here are some of the most recommended and widely respected textbooks for learners at all levels:
- “Linear Algebra Done Right” by Sheldon Axler
- A deep, theory-focused text ideal for math majors.
- “Introduction to Linear Algebra” by Gilbert Strang
- Practical and widely used in engineering programs.
- “Elementary Linear Algebra” by Howard Anton
- Friendly for beginners with extensive examples.
- “Linear Algebra” by Kenneth Hoffman and Ray Kunze
- A classic that balances theoretical depth with clarity.
- “Linear Algebra and Its Applications” by David C. Lay
- Includes real-world problems and applied learning.
🧮 Linear Algebra Examples
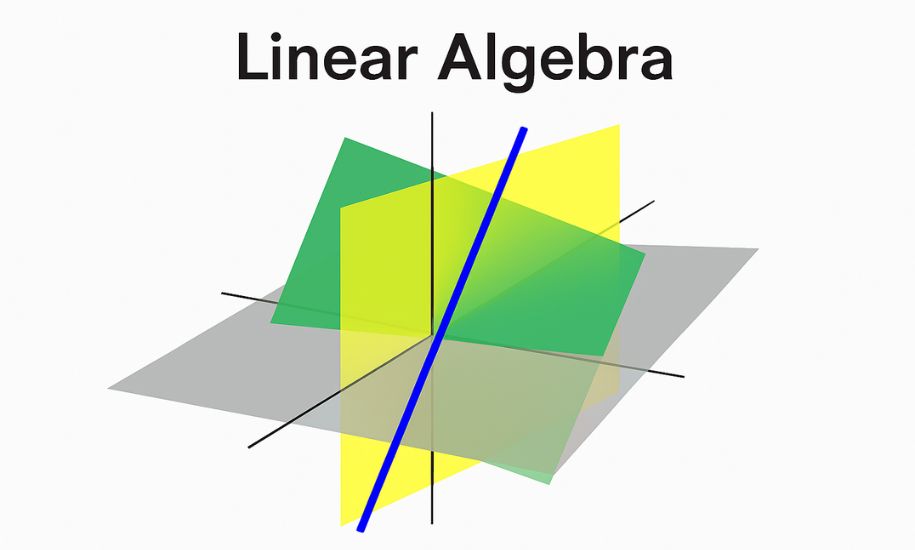
📊 Visual Representation of a Linear System
The image below demonstrates how three planes in three-dimensional space can intersect. This visualization corresponds to a linear system with three variables (x, y, z):
- Each plane represents a linear equation.
- The blue line illustrates the common intersection of all three planes—this line is the solution set to the system.
- If no common line or point exists, the system has no solution or is inconsistent.
Such visuals are essential for understanding the geometric interpretation of systems of equations in linear algebra.
Visual representation of a linear algebra problem involving intersecting planes and a common solution line in 3D space.
📌 Example 1: Solving a System of Equations
2x + 3y = 8
4x - y = 2Convert this into a matrix and solve using Gaussian elimination or inverse matrices. This is foundational in numerical analysis and computational algorithms.
📌 Example 2: Matrix Multiplication
Matrix A (2×2): [[1, 2], [3, 4]]
Matrix B (2×2): [[2, 0], [1, 2]]
Result = AB = [[12+21, 10+22], [32+41, 30+42]] = [[4, 4], [10, 8]]
📌 Example 3: Eigenvalue Calculation
Given matrix A = [[2, 0], [0, 3]], the eigenvalues are simply the diagonal elements: 2 and 3.
📝 Linear Algebra Problems and Solutions
Problem 1: Solve the System
3x + 2y = 16
x - y = 2Solution: Using substitution or matrices:
- From the second equation: x = y + 2
- Substitute into the first: 3(y + 2) + 2y = 16 → 3y + 6 + 2y = 16 → 5y = 10 → y = 2
- Therefore, x = 2 + 2 = 4
Problem 2: Find the Inverse of Matrix
Matrix A:
[ [1, 2],
[3, 4] ]Solution:
- Determinant = (1)(4) – (3)(2) = 4 – 6 = -2
- Inverse = (1/det) * [ [4, -2], [-3, 1] ] = -1/2 * [ [4, -2], [-3, 1] ]
Problem 3: Determine if Vectors Are Linearly Independent
Vectors: v1 = [1, 2], v2 = [2, 4] Solution: v2 = 2 * v1 → They are linearly dependent.
🤖 Mathematics for Machine Learning: Linear Algebra
Linear Algebra forms the mathematical core of machine learning. From training neural networks to optimizing regression models, its role is undeniable.
- Data Representation: Feature sets and datasets are often represented as vectors and matrices.
- Dimensionality Reduction: Techniques like Principal Component Analysis (PCA) rely on eigenvectors and eigenvalues.
- Optimization: Gradient descent and backpropagation algorithms are powered by matrix operations.
- Model Design: Weights, biases, and activation functions in deep learning models depend on linear transformations.
Understanding linear algebra allows machine learning practitioners to better interpret, tweak, and optimize models effectively.
🌐 Applications of Linear Algebra
Linear Algebra is applied extensively in:
- Computer Graphics: Transforming and rendering 3D objects
- Machine Learning: Training models and processing datasets
- Engineering: Structural analysis, robotics, and systems modeling
- Quantum Mechanics: Describing states and transformations
- Economics: Modeling market systems and optimizations
Whether it’s compressing an image or calculating the trajectory of a satellite, linear algebra is the mathematical engine behind it.
🧾 Final Thoughts
Linear Algebra is not just a mathematical discipline—it’s a universal language used to model and solve real-world problems. Whether you’re a student beginning your journey or a professional refining your knowledge, mastering linear algebra opens doors to analytical thinking, problem-solving, and innovation.
For more deep dives into mathematics and structured educational content, visit PureAcad.com — your trusted destination for pure learning and real understanding.